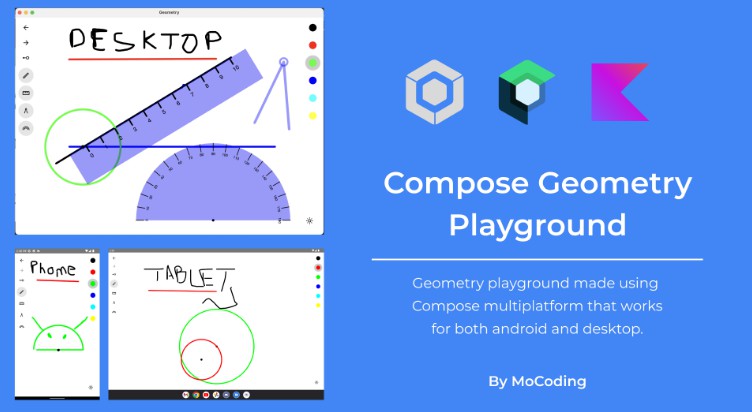
Geometry

Tutorial
Basic syntax
Geometry uses code-like definitions.
Points are represented as complex numbers.
The center of screen is 0 and short side is 200,
so the same code would look the same on all devices.
Lets draw triangle:
A = 20+60i
B = 60-40i
C = -60-40i
t = triangle(A, B, C)
Styles
Lets make our triangle orange, fill it, and make border dashed
A = 20+60i
B = 60-40i
C = -60-40i
[orange] [fill] [dash] t = triangle(A, B, C)
Constructors
In the reality, function triangle expects triangle (and returns it), not three points.
But the following rules work:
- when function expects triangle you can put three points to it
- when function expects segment you can put two point to it
- when function expects line you can put segment or two points to it
- when function expects circle you can put two points (center and some point on circle) to it
- when function expects polygon you can put arbitrary many points to it
ComplexandPointin functions signatures are synonyms
Movable points
Lets allow moving of our points in the view mode:
A = #(20+60i)
B = #(60-40i)
C = #(-60-40i)
[orange] [fill] t = triangle(A, B, C)
Moving by traectory
Lets choose arbitrary point on BC and try to move it:
A = #(20+60i)
B = #(60-40i)
C = #(-60-40i)
[orange] [fill] t = triangle(A, B, C)
D = project(#(-40i), B, C)
Technical details of points moving
When you define X = ... #(...) ...
X will be evaluated as if there is no # and
the anchor for # will be created where X is.
You will be able to move this anchor and expression in parens
will be replaced by position of anchor.
So, the code like X = #(0) + 50 will work contrintuitive.
Animation (dynamic objects)
Your code can use time to animate the drawing.
Lets, for example, animate point D from moving by traectory chapter:
A = #(20+60i)
B = #(60-40i)
C = #(-60-40i)
[orange] [fill] t = triangle(A, B, C)
D = choose(segment(B, C), time()/500)
The choose function chooses a point on given object (segment or circle):
it smoothly moves with second parameter increasing
and reaches initial value when second parameter reaches integer
Ambiguity
Some geometric constructions is ambiguous: they have many results. For example, line and circle intersects in two points.
Such functions have 3 variations:
- returning first (in some not obvious sense) result
- returning second result
- returning other result
To use last way, you must provide one of results. For example, lets intersect line with circle:
O = 0
c = circle(O, 60)
A = cproject(#(45+40i), c)
l = line(A, O)
B = cintersect(A, l, c)
Examples
Installing
Currently, only Windows and Android versions are builded. You can download it here:
For Linux and macOS you can build app from source